Bresenham直线绘图算法：原理与实现

原理图

目前常见的显示设备为光栅化显示器。此类设备采用像素的方式显示图像，也就意味着要在光栅化显示器上画出完美的直线，倾角必须是45k度（k为整数）。

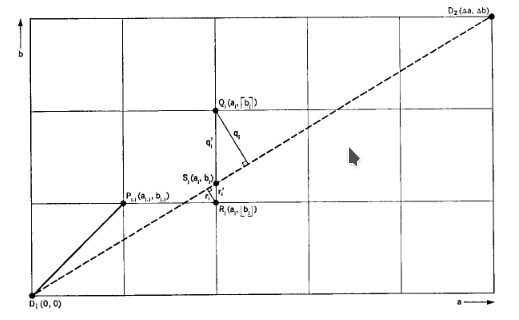
如果不满足角度为45的倍数，需要采用近似的方法，比如，可以选择像素点到实际直线的距离最短者。先考虑斜率介于0和1之间的情况：如上图所示，当$P_i$点被选择为直线的一部分时，$P_{i+1}$只可能是右侧或者右上侧的点。此时，可以由两点到直线的距离之差($r_i-q_i$)的符号判定选择何者。根据相似三角形原理，其符号必然与$r^{\prime}_i-q^{\prime}_i$相同。

又由于$\Delta a > 0$，所以上式符号与$(r^{\prime}_i-q^{\prime}_i)\Delta a$相同。令此变量为“误差值”，记为$\nabla$。Bresenham算法即是通过此误差值的正负来决定下一像素点的选取。但是算法不是每一步都重新计算此值，而是通过递推式更新。这是Bresenham算法高效的原因。

误差值的递推式如下：

$$ \begin{align} \nabla_1 &= 2\Delta b - \Delta a \\ \nabla_{i+1} &= \nabla_i + 2\Delta b - 2\Delta a\quad if \quad \nabla_i \ge 0 \\ \nabla_{i+1} &= \nabla_i + 2\Delta b \quad if \quad \nabla_i < 0 \end{align} $$

递推关系很容易可以证明，如果需要，可以参考Bresenham的原论文，证明非常详细。

现在，我们需要将算法推广到整个二维平面。首先，忽略递推关系的变化，当$\nabla$分别为负和为正时，所对应的下一个像素点不再固定是右侧和右上侧(也就是x加一或者x、y都加一）。但是，x坐标和y坐标的增量可以简单地由线段起始矢量的符号确定。试看下图：

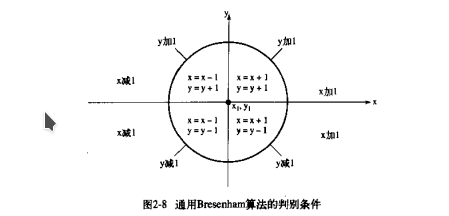
另外，当直线斜率的绝对值大于1时，算法每一步都保证y加一，而不是x加一。这种情况下需要将$\Delta a$ 和$\Delta b$调换，并修改相应的递推式。

说这么多空话可能不容易理解，试结合C++实现与注释理解：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


void bresenham(int x1, int y1, int x2, int y2) { // (x1, y1) to (x2, y2)

    int deltax = std::abs(x1 - x2);
    int deltay = std::abs(y1 - y2);

    const int stepx = x1 < x2 ? 1 : -1; // 根据矢量方向，确定增量大小
    const int stepy = y1 < y2 ? 1 : -1;

    bool steep = false;
    if (deltay > deltax) { // 如果斜率绝对值大于1，交换deltax和deltay
        std::swap(deltax, deltay);
        steep = true;
    }

    int deviation = (deltay << 1) + deltax;

    for (int i = 0; i < deltax; ++i) {
        setpixel(x1, y1); // 选定像素点(x1, y1)

        if (deviation > 0) {
            if (steep) {
                x1 += stepx;
            } else {
                y1 += stepy;
            }

            deviation -= deltax << 1;
        }

        if (steep) {
            y1 += stepy;
        } else {
            x1 += stepx;
        }

        deviation += deltay << 1;
    }
}

以上代码效率可能不足。经过简化后，可以在几行内完成，但可读性下降很多¹：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


void bresenham(int x0, int y0, int x1, int y1) {
    int dx = abs(x1 - x0), sx = x0 < x1 ? 1 : -1;
    int dy = abs(y1 - y0), sy = y0 < y1 ? 1 : -1;
    int err = (dx > dy ? dx : -dy) / 2;

    while (setpixel(x0, y0), x0 != x1 || y0 != y1) {
        int e2 = err;
        if (e2 > -dx) { err -= dy; x0 += sx; }
        if (e2 <  dy) { err += dx; y0 += sy; }
    }
}

用C语言画直线, https://zhuanlan.zhihu.com/p/30553006 ↩︎

Bresenham直线绘图算法：原理与实现

介绍Bresenham光栅化直线绘图算法，并给出简单的实现

On This Page: